Here is something I wrote a while back while working on the design of anemometers for measuring shear stresses. Part of this work required modelling and compensating for the transfer function of tubing systems. To do this in real time we used TMS320 series DSPs, and I impelemented some large FIR filters using block-floating point FFTs.

This is is a general introduction to the FFT, and also discusses the computation of power spectra and autocorrelation. This document is generated from LaTeX using LaTeXML. Some browsers do not support MathML (ie. Chrome), so the online math display uses MathJax. Conversion is not too bad, though there are some formatting problems eg. with tabbing environments. This PDF version is neater:

Download PDF Version of this document

The Fourier transform allows an arbitrary function to be represented in terms of simple sinusoids. The Fourier transform (FT) of a function $f(t)$ is

$$F(\omega )={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(t)e^{-\mathrm{i}\omega t}dt$$

For this integral to exist, $f$ must be absolutely integrable. That is,

However, it is possible to express the transforms of functions that are not absolutely integrable (e.g. periodic) using the delta function $\delta$. With this expression of the function, if $f$ is a periodic function with period $T$ then its transform is not continuous in $\omega$ but consists of impulses in the frequency domain separated by $1/T$.

The Discrete Fourier Transform (DFT) is the discrete-time equivalent of the Fourier transform. A function sampled over a finite period of time is defined by a time series { $x(0)$, $x(1)$, …, $x(N-1)$ }. The Discrete Fourier Transform (DFT) of $x(t)$ is

$$X(k)=\sum _{n=0}^{N-1}x(n)e^{-\mathrm{i2}\pi nk/N},k=0,1,\mathrm{\dots },N-1$$

(1)

For clarity the constant $W$ is defined,

$$W=e^{-\mathrm{i2}\pi /N}$$

then, the sum becomes:

$$X(k)=\sum _{n=0}^{N-1}x(n)W^{nk}$$

The comparable inverse function is the Inverse Discrete Fourier Transform (IDFT):

$$x(t)=\frac{1}{N}\sum _{k=0}^{N-1}X(k)W^{-nk}$$

Note that when writing series, lower case letters indicate time-series, and upper case letters denote their transforms.

The DFT is useful whenever a sampled function must be transformed between the time- and frequency-domains. Applications of this sort include:

• •

  Computation of power spectra for sampled signals.

• •

  Frequency-domain design of digital filters.

Intensive research into signal processing algorithms during the 1960s led to the development of a class of very efficient algorithms for the DFT. These Fast Fourier-Transform (FFT) algorithms led to new applications such as:

• •

  Digital filtering (convolution).

• •

  Correlation.

In these applications, the frequency-domain is used as an intermediate stage to make time-domain calculations more efficient.

The Fast Fourier Transform (or FFT) is a class of efficient algorithms for computing the DFT. FFT algorithms rely on $N$ being composite (ie. non-prime) to eliminate trivial products. Where $N=r_1.r_2\mathrm{\dots }{r}_n$ the complexity¹¹ When an algorithm has complexity O(n), kn is an upper bound on its run-time, for some constant k. of the FFT is $O(N(r_1+r_2+\mathrm{\dots }+r_n))$. The basic radix-2 algorithm published by Cooley and Tukey (1965) relies on $N$ being a power of 2 and is $O(N{\log }_{2}N)$. Other algorithms exist which give better performance. Higher radix algorithms achieve slightly better factorisation and cut down on loop overheads. Winograd’s fourier transform algorithm is based on very efficient short convolutions (Blahut, 1985). However, the saving from using these algorithms is not more than 40%, and this is at the expense of a more complex program. In addition to saving run-time, the FFT is more accurate than straightforward calculation of the DFT since the number of arithmetic operations is less, reducing the rounding error. Stockham (1966) found that two cascaded 256-point FFTs produced half as much error as a single DFT.

In order to derive the basic FFT, assume that $N$ is non-prime and make the factorisations:

$N=AB$	Composite size
$n=b+aB$	time index
$k=c+dA$	frequency index

where $a$, $b$, $c$ and $d$ are all integers.

Rewrite the DFT sum

	$X(c+dA)$	$=$	${\displaystyle \sum _{n=0}^{N-1}}x(n)W^{n(c+dA)}$
		$=$	${\displaystyle \sum _{b=0}^{B-1}}{\displaystyle \sum _{a=0}^{A-1}}x(b+aB)W^{(b+aB)(c+dA)}$
		$=$	${\displaystyle \sum _{b=0}^{B-1}}{\displaystyle \sum _{a=0}^{A-1}}x(b+aB)W^{bc}{W}^{bdA}{W}^{acB}{W}^{adBA}$

Now $W^{adBA}=W^{adN}=1$, since $a$ and $d$ are both integers. Rearranging the remaining factors gives

$$X(c+dA)=\sum _{b=0}^{B-1}{W}^{bdA}{W}^{bc}\sum _{a=0}^{A-1}x(b+aB)W^{acB}$$

(2)

This complex expression can be readily understood when decomposed into a series of steps.

1. 1.

   $\mathrm{Let}{z}_1(a,b)=x(b+aB).$

2. 2.

   $\mathrm{Let}{z}_2(c,b)={\sum }_{a=0}^{A-1}{z}_1(a,b)W^{acB}.$

3. 3.

   $\mathrm{Let}{z}_3(c,b)=W^{bc}{z}_2(c,b).$

4. 4.

   $\mathrm{Let}{z}_4(c,d)={\sum }_{b=0}^{B-1}{z}_3(c,b)W^{bdA}.$

5. 5.

   $\mathrm{Let}X(c+dA)=z_4(c,d).$

When each substitution is made into the previous expression, the result is identical to Equation 2. However, each step is relatively simple:

1. 1.

   Map the input vector into a 2-dimensional array in row-major order.

2. 2.

   Take the DFTs of the columns in the array.

3. 3.

   Scale each element of the array by a complex exponential.

4. 4.

   Take DFTs of all the rows in the array.

5. 5.

   Now map the 2-dimensional array into the output vector in column-major order.

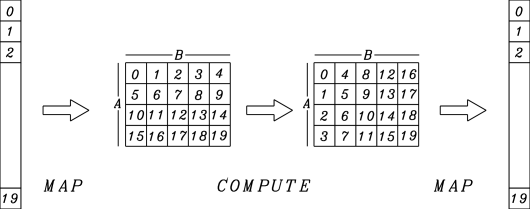
Figure 1 shows the basic structure of the process. The computation takes place on the rows, columns and elements of a 2-D array formed from the original sequence. The $N$ -point DFT has been decomposed into a series of steps.

1. 1.

   Mapping [ $N$ ] $\to$ [ $A$ x $B$ ]

2. 2.

   $B$ $A$ -point DFTs (one per column)

3. 3.

   $N$ complex multiplications

4. 4.

   $A$ $B$ -point DFTs (one per row)

5. 5.

   Mapping [ $A$ x $B$ ] $\to$ [ $N$ ]

Steps 1, 3 and 5 are all O($N$). In the worst case, $A$ and $B$ might be prime and so the DFTs could not be further factorised. In this case the number of complex multiplications is

$$B.A^2+N+A.B^2=N(A+B+1)$$

and additions,

$$BA(A-1)+AB(B-1)=N(A+B-2)$$

so the overall complexity is $O(N(A+B+1))$. If $A$ is composite (eg. equal to $CD$ ) then the $A^2$ representing the contribution of the $A$ -point DFTs can be replaced by $A(C+D)$ giving $O(N(B+C+D))$. Thus it is advantageous to choose $N$ to be highly composite.

The previous discussion involved factorising the DFT when $N$ is non-prime. Cooley and Tukey’s original FFT procedure involves choosing $N=2^L$, for some integer $L$. Putting $A=n/2$ and $B=2$ into equation 2 gives

	$X(c)$	$=$	${\displaystyle \sum _{a=0}^{n/2-1}}x(2a)W^{2ac}+W^c{\displaystyle \sum _{a=0}^{n/2-1}}x(2a+1)W^{2ac}$		(3)
	$X(c+n/2)$	$=$	${\displaystyle \sum _{a=0}^{n/2-1}}x(2a)W^{2ac}-W^c{\displaystyle \sum _{a=0}^{n/2-1}}x(2a+1)W^{2ac}$		(4)

The first equation is for $d=0$ ; the second is for $d=1$. Together, these are the recurrence relations for the decimation-in-time (DIT) FFT. Putting $A=2$ and $B=n/2$ gives instead

	$X(2d)$	$=$	${\displaystyle \sum _{b=0}^{n/2-1}}[x(b)+x(b+n/2)]W^{2bd}$		(5)
	$X(2d+1)$	$=$	${\displaystyle \sum _{b=0}^{n/2-1}}{W}^b[x(b)-x(b+n/2)]W^{2bd}$		(6)

The first equation is for $a=0$ ; the second is for $a=1$. These are the recurrence relations for the decimation-in-frequency (DIF) FFT. These are the two canonical forms of the radix-2 FFT. The computational complexity of the two forms are identical. To illustrate how these relations are used, the structure of the DIT FFT is presented here in a graphical form.

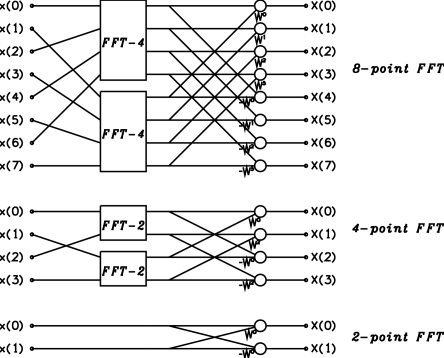
Equation 3 expresses a $N$ -point DFT in terms of two $N/2$ -point DFTs: the DFT of the even terms of the time-series, and the DFT of the odd terms. The equation can be applied recursively to these DFTs until $N=1$, when the transform becomes trivial. Figure 2 shows these relationships graphically. A DFT is represented by a block in the diagram with inputs 0 (top) to $N-1$ (bottom) on the left, and outputs 0 (top) to $N-1$ (bottom) on the right. An open circle denotes a complex addition. A labelled line denotes a complex multiplication by the value of the label. The figure shows the flow-graphs for 8, 4, and 2-point DFTs.

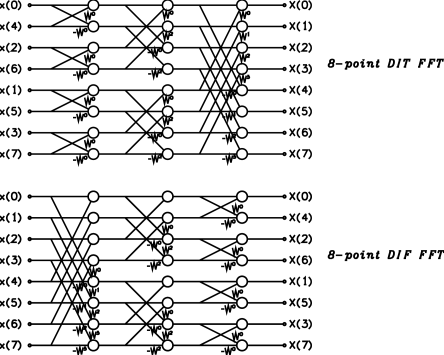
Expanding each of the DFT blocks in Figure 2 gives the graph for the 8-point DIT FFT shown in Figure 3. It also shows the flow graph for the DIF FFT, which can be derived from Equation 5 in a similar way. The major element in the graphs is a pair of parallel line connected by crossing lines. This structure is often termed a “butterfly” calculation, because of its graphical appearance. Each butterfly computation replaces its two inputs with two outputs, without affecting (or being affected by) any other butterfly at the same level in the flow graph. Thus, computation of the FFT can be done in-place with no intermediate storage required. However, the inputs to the DIT FFT (and the outputs of the DIF FFT) are not in the regular order due to the odd/even separation at each stage. In fact, the input terms are in bit-reversed order²² A number is bit-reversed for k digits by writing the k digits of its binary representation (including leading zeros) in reverse order. For example, when k=3, the number 3 (011) bit-reversed is 6 (110). When k=4, 3 (0011) bit-reversed is 12 (1100)., so scrambling (or unscrambling) of the data is an important stage in the transform. In applications where data is transformed, adjusted, and then inverse-transformed it is possible to avoid this scrambling by using the DIT form for the forward transform, and the DIF form for the inverse transform (or vice versa).

The FFT consists of ${\log }_{2}N$ stages, each consisting of $N/2$ butterflies. Each butterfly consists of 2 complex additions and one complex multiplication. Thus the FFT requires $N{\log }_{2}N$ additions and $(N/2){\log }_{2}N$ multiplications and so is $O(N{\log }_{2}N)$. A complex addition consists of 2 real additions. A complex multiplication consists of 4 real multiplications and two real additions. Letting $\alpha$ be the real multiplication time, $\beta$ the real addition time,

$t_{CA}=2\beta$	the time for a complex addition
$t_{CM}=4\alpha +2\beta$	the time for a complex multiplication

Each butterfly takes $2t_{CA}+t_{CM}=4\alpha +6\beta$, and there are $N/2$ butterflies. Thus the proportionality constant for the FFT is

$$t_{fft}=t_{CA}+t_{CM}/2=2\alpha +3\beta$$

and the run-time is

$$t_{fft}N{\log }_{2}N$$

When a series is real, its DFT is hermitian³³A real function $f$, is said to have even symmetry when $f(-x)=f(x)$ and odd symmetry when $f(-x)=-f(x)$. A complex function is said to have hermitian symmetry when $f(-x)=f{(x)}^{*}$, where $*$ denotes the complex conjugate (reflection in the imaginary axis). Note that all real functions are hermitian, but not all hermitian functions are real.. Calculating its DFT directly using the complex DFT involves computing redundant information. There are two optimisations for real series that are dependent on the properties of symmetry and the DFT. They will work with the FFT, but do not depend on it.

Two important processes in signal analysis are

(10)

Suppose that the series $a$, $b$ and $c$ are length $N$. Each of the $N$ values of $k$ in (10) requires an integration over $N$ data points, so the processes are both $O(N^2)$. However, the convolution theorem states that in the frequency domain⁴⁴ Recall that upper-case letters denote the transform of a lower-case series.

(11)

The computation in the frequency domain is $O(N)$. The cost of transforming to and from the frequency domain using the FFT is $O(N{\log }_{2}N)$, which is the most complex part of the process. The speed-up is proportional to $N/{\log }_{2}N$, so for large correlations or convolutions the advantage of the frequency domain computation is considerable. For example, when $N=2^{10}$ the order of the advantage is $2^{10}/10\approx 100$, ie. the time-domain computation is roughly 100 times slower than the frequency-domain computation.
The use of the convolution theorem is not quite as simple as (11) suggests, since using the DFT gives a cyclic convolution. This means that the sums and differences in the index of $b$ in (10) are modulo $N$. The effect of this is to make the first and last data points contiguous, causing the convolution to “wrap around” the end of the record. Thus, even for a short convolution the initial output is affected by the data at the end of the record. This problem is usually solved by appending zeroes to the original series. This cancels the contribution of the terms that “wrap around” from the end of the series, producing an acyclic convolution.

Filtering involves acyclic convolution. The two standard sectioning techniques, which can be found in most DSP textbooks, are the “select-save” procedure (Helms, 1967) and the “overlap-add” procedure (Stockham, 1966). The “select-save” procedure uses overlapped input sections to produce non-overlapping output sections. Some of the computed output is not valid and must be discarded. The “overlap-add” procedure uses non-overlapped input sections to produce overlapping output sections that must be added together. The “overlap-add” method requires slightly more computation (since the output sections must be added) whereas the “select-save” method requires slightly more storage (to store the overlapping input). Otherwise the complexity of the two procedures is identical. The overlap-add procedure is described here.

Suppose that the input sequence $x(n)$ has length $N$. It is to be convolved with the sequence $h(n)$ which represents the inverse transform of the ITF for the system (ie. the impulse response of the correction filter). Suppose $h(n)$ has length $L$. A length $M$ of input section is chosen such that $M\ge L$. $M$ is the length of the transform operations, so if using a radix-2 FFT, it must be a power of 2. The length of the output section is $M+L-1$. The last $L+1$ points of output must be added to the start of the next output section. The function $h(n)$ is modified by appending $M-L$ zeros as follows

Define the $j$ th input section

Each input section is extended to $M$ points as follows

The product

$$W_j(k)=B_j(k)\cdot A(k)$$

gives the cyclic convolution of the two sequences $a(n)$ and $b_j(n)$. However, the modifications ensure that:

1. 1.

   The first $M-L+1$ points of output are correct.

2. 2.

   The last $L-1$ points are contribution of the end of the current section to the start of the next section.

The points in (2) are added to the start of the output for section $x_{j+1}$. The algorithm can be summarised as follows. Suppose that $y(n)$ is the output of the convolution.

(1)	Form $a(n)$ and compute its transform $A(k)$
(2) .	For $j$ = $0$ to $N/(M-L+1)$ do
.	a)	Form $b_j(n)$ and compute the DFT $B_j(k)$
.	b) .	Calculate $W_j=A(k)\cdot B_j(k)$
.	c) .	Compute the IDFT $w_j(n)$
.	d) .	Let $w_{j^{\prime }}(n)=w_j(n)+w_{j-1^{\prime }}(M-L+1+n)$ for
.	e) .	Let $y_j(n)=w_{j^{\prime }}(n)$ for $0\le n\le M-L$

The convolution is computed with $2N/(M-L+1)$ FFT operations. The computation time per sample for complex data is thus

$$T=\frac{2t_{fft}M{\log }_{2}M+M{t}_{CM}}{(M-L+1)}$$

The optimal values of $L$ and $M$ can be found by minimising this expression. According to Helms (1967) the optimal value of $M$ is approximately $L{\log }_{2}L$ but departures from this value can be made without greatly increasing the running time.

Estimation of autocorrelation and power spectra are classical problems and are well described in the literature (Oppenheim and Schafer, 1975; Geçinki and Yavuz, 1983). They are closely related, since the power spectrum is the fourier transform of the autocorrelation. Two techniques for estimation of power spectra are:

(1) The indirect method - First, the autocorrelation of the sequence is computed. This can be done in the time-domain or in the frequency domain (using the FFT). The autocorrelation function is then transformed into the frequency domain, giving the power spectrum. To reduce leakage, the autocorrelation function is multiplied by a window before transformation.

(2) The direct method - A short section of the input is transformed into the frequency domain (using the FFT). The transformed values are each multiplied by their complex conjugate, giving an estimate of the power spectrum for that section. The process is repeated for a number of sections and the results are added to give the final power spectrum. To reduce leakage, each section of the time-domain data is multiplied by a window function before transformation. This technique is due originally to Welch (1967).

Window functions are necessary to reduce leakage in the power spectrum. The direct method appears to be more efficient, but the transform of its spectral estimator is a measure of cyclic correlation. If only the power spectrum is desired, the direct method is more efficient. However, if both the autocorrelation and the power spectrum are desired the indirect method is preferred. It also gives lower variance in the estimate (Geçinki and Yavuz, 1983).

An efficient algorithm for computing autocorrelation is given by Rader (1970). Suppose that $x(n)$ is the input sequence of length $N$. The inverse transform of $X(k)X^{*}(k)$ gives the cyclic autocorrelation. To get a linear correlation, an equal number of zeros must be appended to the input sequence. However, in practice $N$ is very large compared with the number of lags desired. In this, the data can be processed in smaller sections (as described in section 6). Let $x_j(n)$ denote a length $M$ sequence formed by taking $M/2$ points from $x$ and appending $M/2$ zeros as follows

Let

In the frequency domain form the product

$$W_j=X_j{}^{*}(k)\cdot Y_j(k)$$

The first $M/2$ elements of $w_j$ represent the contribution of the $j$ th section of $x$ to the autocorrelation. Let

$$Z_j(k)=\sum _{m=0}^j{W}_m(k)=Z_{j-1}(k)+W_j(k)$$

Then the autocorrelation is given by

$$R(k)=(1/N)IDFT\{Z_{(2N/M)-1}(k)\}$$

Rader employs the simplification

$$Y_j(k)=X_j(k)+{(-1)}^k{X}_{j+1}(k)$$

Thus, it is never necessary to form the sequence $y_j(n)$ or take its transform $Y_j(k)$ so the required number of DFT operations is halved. Multiplying a DFT by ${(-1)}^k$ corresponds to a shift in time of $M/2$ positions. Rader’s efficient algorithm can be summarised:

(1)	Form $x_0(n)$ and calculate its transform $X_0(k)$
.	Let $Z_0(k)=0$, for
(2) .	For do
.	a)	Form $x_{j+1}(n)$ and compute $X_{j+1}(k)$
.	b) .	compute $Z_{j+1}(k)=Z_j(k)+X_j^{*}(k)[X_j(k)+{(-1)}^k{X}_{j+1}(k)]$
(3) .	Let $R(s)=\frac{1}{N}IDFT(Z_{2N/M-1}(k))$
.	keeping only the first $M/2+1$ values.

Thus the autocorrelation is computed with $2N/M$ DFT operations (including the final IDFT). However, the number of lag values is not rigidly tied to the transform length $M$. Lag values $pM/2\le s\le (p+1)M/2$ can be obtained by accumulating

$$Z_{j+1}{}^p(k)=Z_j{}^p(k)+X_j{}^{*}(k)[X_{j+p}(k)+{(-1)}^k{X}_{j+p+1}(k)]$$

Suppose that $L$ lag values are desired. The computation time (using the complex FFT) per sample is

	$t_R$	$=$	${\displaystyle \frac{2}{M}}(t_{fft}M{\log }_{2}M+t_{CMA}L)$
		$=$	$2t_{fft}{\log }_{2}M+2t_{CMA}L/M$

where $t_{CMA}=2t_{CA}+t_{CM}$ is the time per point to compute 2(b) above. $t_R$ can be minimised by choosing $M$ appropriately. Analytically, the minimum based on a zero derivative is

$$M=L{t}_{cma}\ln (2)/t_{fft}$$

With the complex FFT, $t_{CMA}/t_{fft}=2$, so optimum performance obtains when $M\approx 1.38L$. With the real FFT (for large $M$) $t_{CMA}/t_{fft}\approx 4$ so $M\approx 2.77L$. Using the radix-2 FFT, $M$ and $N$ must be powers of 2, so if $M=2.77L$, $L=2^n$, and $M=2^m$

	$2^m$	$=$	$\ln (2)t_{CMA}/t_{fft}{2}^n$
	$m-n$	$=$	${\displaystyle \frac{\ln (\ln (2)t_{CMA}/t_{FFT})}{\ln (2)}}$

Thus, for $M=2.77L$, $m\approx n+1$.